Integrating both sides. Each row in the solution array y corresponds to a value returned in column vector t.

How To Solve Differential Equations Differential Equations Equations Solving
Dx dt 3x2ycos2t We will use the ode45 command to solve the system of first order differential equations.

. When you are solving a DAE you can specify initial conditions for both y 0 and y 0. Calculator applies methods to solve. Given the following inputs.
X dy dt Thus we can rewrite the differential equation as. Solve an Initial Value Problem Using a Greens Function Solve a Boundary Value Problem Using a Greens Function Solve the Wave Equation Using Its Fundamental Solution. An example of using ODEINT is with the following differential equation with parameter k03 the initial condition y 0 5 and the following differential equation.
In the equation represent differentiation by using diff. Specify a differential equation by using the operator. Differential equation or system of equations specified as a symbolic equation or a vector of symbolic equations.
It involves a derivative dydx. There are many tricks to solving Differential Equations if they can be solvedBut first. D 2 ydx 2 Px dydx Qxy fx.
A first order ode has the form Fxyy0 0. An ordinary differential equation that defines the value of dydx in the form x and y. The solvers all use similar syntaxes.
Separable homogeneous linear first-order Bernoulli Riccati integrating factor differential grouping reduction of order inhomogeneous constant coefficients Euler and systems differential equations. The ode23s solver only can solve problems with a mass matrix if the mass. 721 Solution Methods for Separable First Order ODEs g x dx du x h u Typical form of the first order differential equations.
The model initial conditions and time points are defined as inputs to. All MATLAB ODE solvers can solve systems of equations of the form y f t y or problems that involve a mass matrix M t y y f t y. A differential equation is an equation involving a function and its derivatives.
An equation with the function y and its derivative dy dx. A Differential Equation is a n equation with a function and one or more of its derivatives. Variation of Parameters which is a little messier but works on a wider range of functions.
It can be referred to as an ordinary differential equation ODE or a partial differential equation PDE depending on whether or not partial derivatives are involved. Undetermined Coefficients which only works when fx is a polynomial exponential sine cosine or a linear combination of those. So we proceed as follows.
Without or with initial conditions Cauchy problem Enter expression and press or the button. Why Are Differential Equations Useful. We saw the following example in the Introduction to this chapter.
71 in which hu and gx are given functions. Linear differential equations are ones that can be manipulated to look like this. Dydxx2-3 As we did before we will integrate it.
First order differential equations are differential equations which only include the derivative dfracdydx. Xn i1 c iu ixy will also solve the equation. We will give a derivation of the solution process to this type of differential equation.
To solve the separable equation y0 MxNy we rewrite it in the form fyy0 gx. Denoting the partial derivative of u x u x and u y u. If eqn is a symbolic expression without the right side the solver assumes that the right side is 0 and solves the equation eqn 0.
The term ordinary is used in contrast. If Gxy can be factored to give Gxy MxNythen the equation is called separable. In theory at least the methods of algebra can be used to write it in the form y0 Gxy.
Where Px Qx and fx are functions of x by using. We solve it when we discover the function y or set of functions y. Well also start looking at finding the interval of validity for the solution to a differential equation.
Yt The Python code first imports the needed Numpy Scipy and Matplotlib packages. There are no higher order derivatives such as dfracd2ydx2 or dfracd3ydx3 in these equations. An ordinary differential equation ODE is an equation containing an unknown function of one real or complex variable x its derivatives and some given functions of xThe unknown function is generally represented by a variable often denoted y which therefore depends on xThus x is often called the independent variable of the equation.
Yintx2-3dx and this gives yx33. Differential equations in the form Ny y Mx. In this section we solve separable first order differential equations ie.
D2y dt2 3 dy dt 2ycos2t or in terms of x. For 0 t 10 we must define a variable x such that. The task is to find the value of unknown function y at a given point x ie.
A homogeneous linear differential equation is a differential equation in which every term is of the form. DAEs arise in a wide variety of systems because physical conservation laws often have forms like x y z 0If x x y and y are defined explicitly in the equations then this conservation equation is sufficient to solve for z without having an expression for z. Examples of Differential Equations Example 1.
Which is an unknown function in more than one variable xy. The linear equation 19 is called homogeneous linear PDE while. In this section well define boundary conditions as opposed to initial conditions which we should already be familiar with at this point and the boundary value problem.
We will also work a few examples illustrating some of the interesting differences in using boundary values instead of initial conditions in solving differential equations. We can solve a second order differential equation of the type. By rearranging the terms in Equation 71 the following form with the lefthandside LHS.
Fracdytdt -k. PARTIAL DIFFERENTIAL EQUATIONS Math 124A Fall 2010 Viktor Grigoryan grigoryanmathucsbedu. Initial value of y ie y0.
This will be a general solution involving K a constant of integration.

Rbse Solutions For Class 12 Maths Chapter 12 Differential Equation Ex 12 8 Https Www Rbsesolutions Com Clas Class 12 Maths Studying Math Learning Mathematics

How To Solve Differential Equations Differential Equations Equations Solving Equations

Homogeneous Differential Equation Xdx Y 2x Dy 0 Differential Equations Math Videos Equation
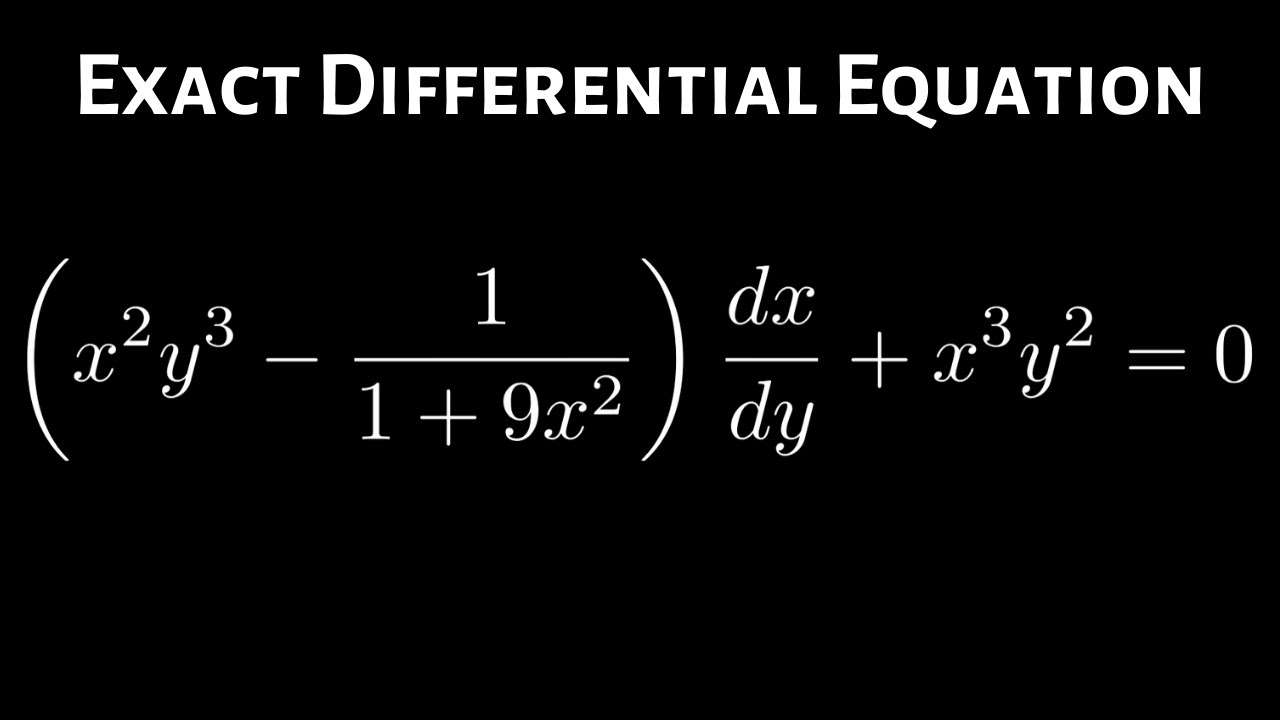
Exact Differential Equation X 2y 3 1 1 9x 2 Dx Dy X 3y 2 0 Differential Equations Math Videos Mathematics

Reduction Of Order Linear Second Order Homogeneous Differential Equations Differential Equations Equations Math

Solve A Linear Second Order Homogeneous Differential Equation Initial Va Differential Equations Solving Equations Solving

How To Solve A Differential Equation With Series X 1 Y Xy Y Differential Equations Math Videos Solving

Solving The Bernoulli Differential Equation X 2 Dy Dx Y 2 Xy Math Videos Maths Exam Differential Equations

System Of Differential Equations By Elimination Ex1 Differential Equations Equations Linear Differential Equation

Homogeneous Linear Third Order Differential Equation Y 7y 8y 0 Differential Equations Math Videos Equations

Homogeneous Differential Equation X Y Dx Xdy 0 Differential Equations Math Videos Equations

Separable Differential Equation X Dy Dx 8y Differential Equations Math Videos Mathematics

Chegg Com Physics And Mathematics Math Formula Chart College Algebra

How To Solve Differential Equations Differential Equations Equations Solving Equations

Solve The Given Differential Equation By Separation Chegg Com Math Formulas Studying Math Math

Variation Of Parameters Y Y Sec X Math Videos Differential Equations Solving

Intro To Initial Value Problems 2 Differential Equations Differential Equations Equations Intro

Ex 1 Solve A Linear Second Order Homogeneous Differential Equation Ini Differential Equations Solving Equations

